27. Фундаментальная система решений однородной СЛУ: определение, теорема.
Множество решений однородной линейной системы относительно n неизвестных является линейным подпространством пространства Rn. Размерность этого подпространства равна n − r, где r − ранг матрицы системы A.
Любой базис пространства решений однородной системы линейных уравнений называется фундаментальной системой решений однородной системы.
Иначе говоря, любая упорядоченная совокупность n − r линейно независимых решений однородной линейной системы образует фундаментальную систему решений однородной системы.
Например: Однородная система линейных алгебраических уравнений
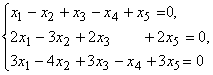
с помощью элементарных преобразований может быть приведена к каноническому виду:
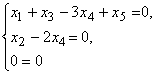
Ранг r матрицы равен 2, число n неизвестных равно 5, система нетривиально совместна. Размерность пространства решений этой однородной системы равна 3: d = n − I = 5 − 2 = 3.
три линейно независимые решения системы

образуют базис пространства решений системы, т.е. образуют её фундаментальную систему решений.
Добавил: Гаврюша

